이진 트리(Binary Tree)

in CS study / Algorithm

이진 트리(Binary Tree) 관련 개념 정리글 입니다.

이진 트리는 다양한 응용 프로그램에서 널리 사용되는 컴퓨터 과학의 중요한 데이터 구조이다. 데이터를 계층 구조로 저장하고 검색하는 효율적인 방법을 제공하며 검색 및 정렬 알고리즘을 구현하고 컴퓨터 과학의 복잡한 문제를 해결하는 데 사용할 수 있다.

정의

  • 정의: 이진 트리(Binary Tree)는 모든 노드의 차수가 2 이하인 트리(Tree) 자료구조의 일종이다. 즉, 각 노드는 최대 두 개의 자식 노드를 가질 수 있다.

  • 이진 트리는 루트(Root) 노드부터 시작하여 각 노드가 왼쪽 자식 노드와 오른쪽 자식 노드를 갖는 구조로 이루어져 있다. 이진 트리는 이진 탐색 트리(Binary Search Tree), AVL 트리(AVL Tree), 레드-블랙 트리(Red-Black Tree) 등 다양한 자료구조의 기반이 되며, 이진 탐색(Binary Search) 알고리즘 등에 활용된다.

특성

이진트리(Binary Tree)는 다음과 같은 특성을 가지고 있다.

  • 각 노드는 최대 두 개의 자식 노드를 가질 수 있다.
  • 이진트리의 노드들은 왼쪽 서브트리(Left Subtree)와 오른쪽 서브트리(Right Subtree)로 나누어진다.
  • 서브트리 또한 이진트리여야 한다.
  • 중복된 노드가 존재하지 않는다.
  • 이진트리의 깊이(Depth)가 \(h\)일 때, 최대 노드의 개수는 \(2^{h} - 1\)이다.
  • 이진트리의 노드 수가 \(n\)일 때, 최소 높이는 \(log₂(n+1)\)이다.
  • 이진트리의 순회(Traversal)는 전위 순회(Preorder Traversal), 중위 순회(Inorder Traversal), 후위 순회(Postorder Traversal)로 이루어진다.

Tree traversal algorithms

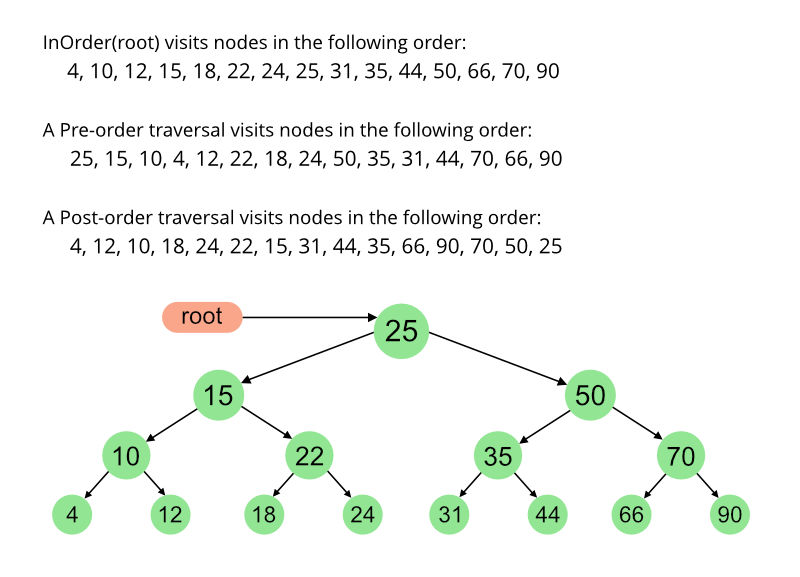
treetraversal

Tree traversal algorithms 예시

1. 전위 순회(Preorder Traversal)

  • 루트 노드를 먼저 방문하고, 왼쪽 서브트리를 전위 순회한 후, 오른쪽 서브트리를 전위 순회한다.
  • 노드의 값을 읽는 순서: 루트 - 왼쪽 - 오른쪽
  • 전위 순회는 트리의 구조를 파악하는 데 유용
class Node:
	def __init__(self, key):
		self.left = None
		self.right = None
		self.val = key


# A function to do preorder tree traversal
def printPreorder(root):

	if root:

		# First print the data of node
		print(root.val),

		# Then recur on left child
		printPreorder(root.left)

		# Finally recur on right child
		printPreorder(root.right)


# Driver code
if __name__ == "__main__":
    root = Node(1)
    root.left = Node(2)
    root.right = Node(3)
    root.left.left = Node(4)
    root.left.right = Node(5)

    # Function call
    print "Preorder traversal of binary tree is"
    printPreorder(root)

#output
# Preorder traversal of binary tree is 
# 1 2 4 5 3

전위 순회(Preorder Traversal) 예시 코드

2. 중위 순회(Inorder Traversal)

  • 왼쪽 서브트리를 중위 순회한 후, 루트 노드를 방문하고, 오른쪽 서브트리를 중위 순회한다.
  • 노드의 값을 읽는 순서: 왼쪽 - 루트 - 오른쪽
  • 중위 순회는 이진 탐색 트리에서 정렬된 순서대로 노드를 읽는 데 사용
class Node:
	def __init__(self, key):
		self.left = None
		self.right = None
		self.val = key


# A function to do inorder tree traversal
def printInorder(root):

	if root:

		# First recur on left child
		printInorder(root.left)

		# then print the data of node
		print(root.val),

		# now recur on right child
		printInorder(root.right)


# Driver code
if __name__ == "__main__":
	root = Node(1)
	root.left = Node(2)
	root.right = Node(3)
	root.left.left = Node(4)
	root.left.right = Node(5)

	# Function call
	print "\nInorder traversal of binary tree is"
	printInorder(root)

#output
# Inorder traversal of binary tree is 
# 4 2 5 1 3

중위 순회(Inorder Traversal) 예시 코드

3. 후위 순회(Postorder Traversal)

  • 왼쪽 서브트리를 후위 순회한 후, 오른쪽 서브트리를 후위 순회한 후, 루트 노드를 방문한다.
  • 노드의 값을 읽는 순서: 왼쪽 - 오른쪽 - 루트
  • 후위 순회는 트리에서 자식 노드들을 모두 방문한 후 부모 노드를 방문하기 때문에, 트리의 제거 작업 등에서 유용
class Node:
	def __init__(self, key):
		self.left = None
		self.right = None
		self.val = key

# A function to do postorder tree traversal
def printPostorder(root):

	if root:

		# First recur on left child
		printPostorder(root.left)

		# the recur on right child
		printPostorder(root.right)

		# now print the data of node
		print(root.val),


# Driver code
if __name__ == "__main__":
    root = Node(1)
    root.left = Node(2)
    root.right = Node(3)
    root.left.left = Node(4)
    root.left.right = Node(5)

    # Function call
    print "\nPostorder traversal of binary tree is"
    printPostorder(root)

#output
# Postorder traversal of binary tree is 
# 4 5 2 3 1

후위 순회(Postorder Traversal) 예시 코드

4. 레벨 순회(Level-order Traversal)

  • 루트 노드부터 시작하여 한 레벨씩 내려가면서 왼쪽에서 오른쪽으로 모든 노드를 방문한다.
  • 노드의 값을 읽는 순서: 상위 레벨부터 순서대로(좌에서 우로)
  • 레벨 순회는 트리에서 너비 우선 탐색(Breadth-First Search)을 수행하는 데 사용

참고 문헌 및 사이트