삽입 정렬(Insertion Sort)
삽입 정렬(Insertion Sort) 관련 개념 정리글 입니다.
삽입 정렬(Insertion Sort)은 간단하면서도 효율적인 정렬 알고리즘 중 하나이다.
개념 및 정의
삽입 정렬은 정렬된 부분을 점진적으로 늘려가며 정렬을 완성하는 방식으로 동작한다. 이 알고리즘은 선택 정렬과 유사한 방법이지만, 선택 정렬은 최솟값을 찾아 앞으로 이동하는 반면, 삽입 정렬은 정렬된 부분에 적절한 위치에 삽입하는 방식으로 동작한다.
동작 방식
- 주어진 배열을 정렬된 부분과 정렬되지 않은 부분으로 나눈다. 초기에는 첫 번째 원소만 정렬된 부분에 속하고, 나머지는 정렬되지 않은 부분이다.
- 정렬되지 않은 부분의 첫 번째 원소를 정렬된 부분의 알맞은 위치에 삽입한다. 이를 위해 정렬된 부분에서 원소를 비교하고, 삽입할 위치를 찾아 원소들을 오른쪽으로 한 칸씩 이동시킨다.
- 나머지 정렬되지 않은 원소들도 동일한 방식으로 정렬된 부분에 삽입하면서 정렬을 완성해간다.
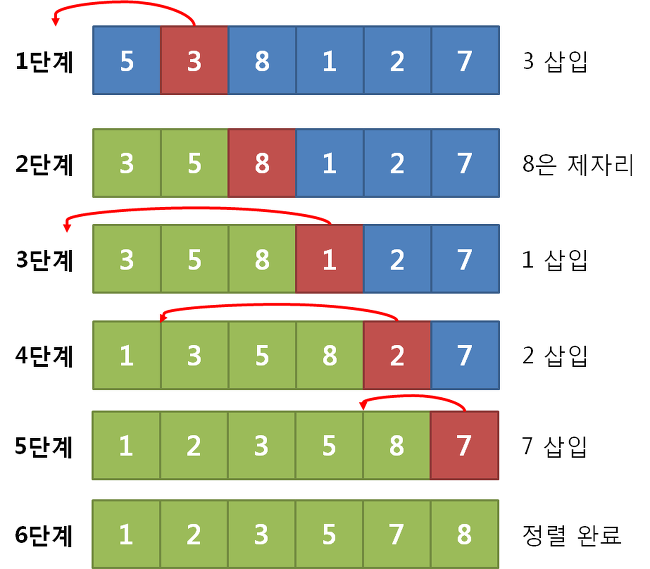
Insertion Sort 동작 방식
특징
장점
- 구현이 간단하고 이해하기 쉽다.
- 작은 규모의 입력 데이터에 대해서는 효율적이다.
- 안정적인 정렬 알고리즘이다.
- 제자리 정렬(in-place sorting)로, 입력 배열 외에 추가적인 메모리 공간을 요구하지 않는다.
단점
- 최악의 경우에는 다른 비교 기반 정렬 알고리즘에 비해 상대적으로 느리다.
- 최악의 경우 시간 복잡도는 \(O(n^{2})\)이다.
- 입력 크기가 크고 무작위로 정렬되지 않은 경우에는 비효율적이다. 다른 알고리즘보다 더 많은 비교 및 이동 연산이 필요하다.
- 비교 기반 정렬 알고리즘 중 하나로, 큰 데이터셋이나 성능 요구가 높은 상황에서는 좋지 않다.
구현 방법
- 삽입 정렬 알고리즘 – 반복 접근 방식
# Python program for implementation of Insertion Sort
# Function to do insertion sort
def insertionSort(arr):
# Traverse through 1 to len(arr)
for i in range(1, len(arr)):
key = arr[i]
# Move elements of arr[0..i-1], that are
# greater than key, to one position ahead
# of their current position
j = i-1
while j >= 0 and key < arr[j] :
arr[j + 1] = arr[j]
j -= 1
arr[j + 1] = key
# Driver code to test above
arr = [12, 11, 13, 5, 6]
insertionSort(arr)
for i in range(len(arr)):
print ("% d" % arr[i])
#output
#5 6 11 12 13
삽입 정렬(반복 방식) 구현 코드 예시 (시간 복잡도 \(O(n^{2})\))
시간 복잡도 분석
최선의 경우(입력이 이미 정렬되어 있는 경우) 외부 반복문에서 한 번씩만 비교하면서 삽입 위치를 찾게 되므로, 내부 반복문은 한 번도 수행되지 않는다. 따라서 외부 반복문의 실행 횟수는 \(n-1\)번이 된다. 이 경우 시간 복잡도는 \(O(n)\)이다.
최악의 경우(입력이 역순으로 정렬되어 있는 경우) 외부 반복문에서 \(i\)번째 원소를 정렬된 부분과 비교하는 경우, \(i\)번째 원소를 삽입하기 위해 최대 \(i\)번의 비교 연산이 수행된다. 이 때, \(i\)는 \(1\)부터 \(n-1\)까지 변화하므로 내부 반복문의 실행 횟수는 최악의 경우 \(1 + 2 + 3 + ... + (n-1)\)번이 된다. 이는 등차수열의 합으로 계산하면 \((n-1) * (n-1+1) / 2 = n^{2}/2 - n/2\)이 된다. 따라서 최악의 경우 시간 복잡도는 \(O(n^{2})\)이다.
평균적인 경우 입력이 무작위로 주어진 경우, 각 원소를 삽입할 위치를 찾기 위해 평균적으로 \(\frac{n}{2}\)번의 비교가 수행된다. 외부 반복문은 \(n-1\)번 실행되므로, 전체적인 시간 복잡도는 \(O(n^{2})\)이다.
