배열(Array) & 연결 리스트(Linked List)
배열(Array)과 연결 리스트(Linked List) 관련 개념 정리글 입니다.
자료구조에서 배열과 연결리스트는 기본적으로 알고있어야하는 중요한 개념이다.
배열(Array)
정의
- 배열은 동일한 데이터 타입의 원소들을 연속적으로 메모리에 저장하는 자료구조이다.
- 배열은 인덱스를 사용하여 각 원소에 접근할 수 있다.
- 배열은 정적으로 크기가 지정되며, 크기는 선언 시에 결정된다.
특징
장점
- 빠른 인덱스 기반 접근: 배열은 원소에 대한 인덱스를 사용하여 \(O(1)\)의 시간 복잡도로 접근할 수 있다.
- 메모리 캐시 효율성: 배열은 원소들이 메모리에 연속적으로 저장되어 있기 때문에 캐시 메모리 활용이 용이하며, 접근 시간이 빠르다.
- 고정 크기로 선언: 배열은 크기가 고정되어 있어 메모리 할당 및 해제에 대한 오버헤드가 적다.
- 연속적인 메모리 구조: 인덱스를 통한 접근과 연속적인 메모리 구조로 인해 데이터의 저장과 탐색이 효율적이다.
단점
- 크기 조정의 어려움: 배열은 선언 시에 크기를 지정하고, 크기를 변경하기 어렵다.
- 삽입 및 삭제의 비효율성: 배열은 원소를 삽입하거나 삭제할 때에는 해당 위치에 있는 원소들을 이동시켜야 하므로 비효율적이다. (\(O(n)\)의 시간 복잡도)
- 메모리 낭비 가능성: 배열은 크기가 고정되어 있기 때문에, 미리 큰 크기로 할당하면 사용하지 않는 공간이 낭비될 수 있다.
시간 복잡도
- 탐색
- \(O(1)\) (단, 접근하고자 하는 인덱스를 알고 있어야 한다. 순차적으로 탐색시에는 \(O(n)\))
- 삽입 / 삭제
- 배열의 처음 또는 중간에 삽입 및 삭제 : \(O(n)\) (삽입 지점 이후의 데이터를 옮겨야 하기 때문)
- 배열의 끝에 삽입 및 삭제 : \(O(1)\)
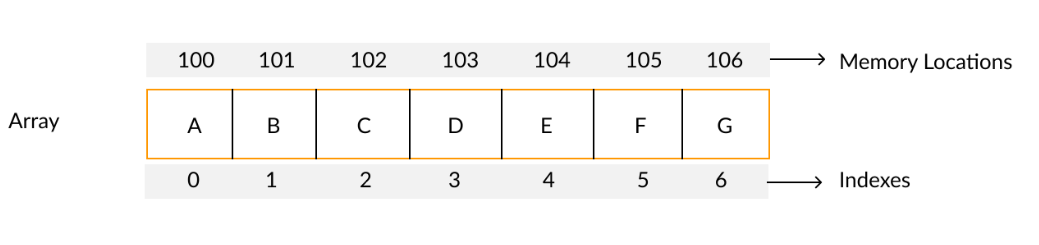
배열(Array)
연결 리스트(Linked List)
정의
- 연결 리스트는 각 노드가 데이터와 다음 노드를 가리키는 포인터로 구성된 자료구조이며, 첫번째 노드를 head, 마지막 노드를 tail이라고 한다.
- 각 노드는 데이터와 다음 노드를 가리키는 포인터로 이루어져 있으며, 마지막 노드는 일반적으로 NULL을 가리키는 포인터를 가진다.
- 연결 리스트는 동적으로 크기가 조정되며, 요소들이 메모리에 불연속적으로 저장된다.
특징
장점
- 동적 크기 조정: 연결 리스트는 동적으로 크기를 조정할 수 있어 메모리 사용을 효율적으로 관리할 수 있다.
- 삽입/삭제의 용이성: 연결 리스트에서는 새로운 노드를 삽입하거나 노드를 삭제할 때, 단순히 포인터의 변경만으로 수행할 수 있어 효율적이다.
- 메모리 공간의 효율성: 연결 리스트는 각 노드가 데이터와 포인터만을 저장하기 때문에 메모리 공간을 효율적으로 활용할 수 있다.
단점
- 느린 접근 시간: 연결 리스트에서 특정 위치에 있는 노드에 접근하기 위해서는 처음부터 순차적으로 탐색해야 하므로 접근 시간이 느리다.
- 추가적인 메모리 오버헤드: 각 노드마다 포인터를 가지고 있어 추가적인 메모리 오버헤드가 발생한다.
- 순차 접근만 가능: 연결 리스트는 순차적인 탐색에 최적화되어 있으며, 임의의 위치로 직접 접근하는 것이 어렵다.
시간 복잡도
탐색 : \(O(n)\)
삽입 / 삭제: 삽입과 삭제 자체는 \(O(1)\)이다.
- 연결 리스트의 처음에 삽입/삭제 : \(O(1)\)
- 연결 리스트의 중간에 삽입/삭제 : \(O(n)\) (탐색시간 소요)
- 연결 리스트의 끝에 삽입/삭제 :
- 끝을 가리키는 별도의 포인터를 갖는 경우 : \(O(1)\)
- 끝을 가리키는 별도의 포인터를 갖지 않는 경우 : \(O(n)\) (탐색시간 소요)
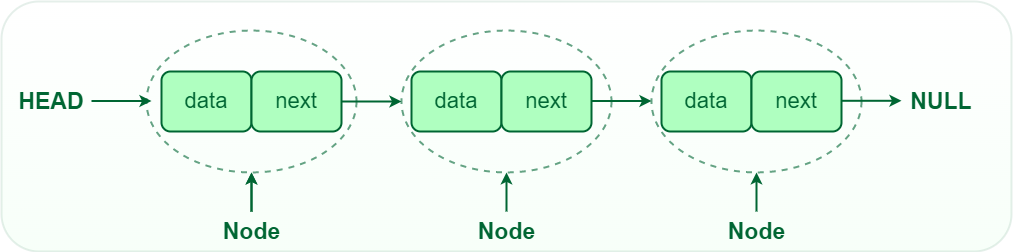
연결 리스트(Linked List)
배열과 연결리스트 비교
- 장점
- 배열 : 인덱스를 통한 빠른 접근 가능하다
- 연결 리스트 : 삽입/삭제가 용이하다
- 단점
- 배열 : 삽입/삭제가 오래 걸리고, 배열 중간에 있는 데이터가 삭제되면 공간 낭비가 발생한다
- 연결 리스트 : 임의 접근이 불가능하여, 처음부터 탐색을 진행해야 한다
- 용도
- 배열 : 빠른 접근이 요구되고, 데이터의 삽입과 삭제가 적을 때 용이하다
- 연결 리스트 : 삽입과 삭제 연산이 잦고, 검색 빈도가 적을 때 용이하다
연결리스트 순회/삽입/삭제 구현
class Node:
def __init__(self, item):
self.data = item
self.next = None
class LinkedList:
def __init__(self):
self.nodeCount = 0
self.head = None
self.tail = None
def getAt(self, pos):
if pos < 1 or pos > self.nodeCount:
return None
i = 1
curr = self.head
while i < pos:
curr = curr.next
i += 1
return curr
def insertAt(self, pos, newNode): #삽입
if pos < 1 or pos > self.nodeCount + 1:
return False
if pos == 1:
newNode.next = self.head
self.head = newNode
else:
if pos == self.nodeCount + 1:
prev = self.tail
else:
prev = self.getAt(pos - 1)
newNode.next = prev.next
prev.next = newNode
if pos == self.nodeCount + 1:
self.tail = newNode
self.nodeCount += 1
return True
def popAt(self, pos): #삭제
if pos < 1 or pos > self.nodeCount:
raise IndexError
node = self.getAt(pos)
if self.nodeCount == 1 & pos == 1:
self.head = None
self.tail = None
elif pos == 1:
self.head = self.getAt(pos+1)
else:
prev = self.getAt(pos-1)
if pos == self.nodeCount:
prev.next = None
self.tail = prev
else:
prev.next = prev.next.next
self.nodeCount -= 1
return node.data
def traverse(self): #탐색
result = []
curr = self.head
while curr is not None:
result.append(curr.data)
curr = curr.next
return result
연결 리스트 순회/삽입/삭제 코드 구현
이중 연결리스트
이중 연결 리스트의 개념과 구조
- 이중 연결 리스트의 정의: 이중 연결 리스트는 각 노드가 데이터와 이전 노드를 가리키는 포인터, 그리고 다음 노드를 가리키는 포인터로 구성된 자료구조이다.
- 이중 연결 리스트의 구조: 각 노드는 이전 노드와 다음 노드를 모두 가리킬 수 있으므로, 양방향으로 탐색이 가능하다.
이중 연결 리스트의 특징
- 장점
- 양방향으로 순회할 수 있어 이전 노드로의 접근이 용이하다.
- 삽입/삭제 연산이 단일 연결 리스트보다 효율적으로 수행될 수 있다.
- 단점
- 추가적인 포인터를 저장해야 하므로 메모리 공간이 더 필요하다.
- 포인터의 조작이 필요하여 단일 연결 리스트에 비해 약간의 오버헤드가 발생할 수 있다.
- 장점
시간 복잡도
탐색: 최악의 경우 \(O(n)\) 시간이 소요된다. (양방향으로 순회가 가능하므로 일반적인 경우에는 \(O(n/2)\) 시간에 탐색이 가능하다.)
삽입/삭제: 특정 노드를 삽입하거나 삭제하는 경우 해당 노드의 이전 노드와 다음 노드를 조작하므로 \(O(1)\) 시간이 소요된다. 하지만 특정 위치에 삽입하거나 삭제하는 경우에는 먼저 탐색해야 하므로 삽입/삭제 연산의 평균 시간 복잡도는 \(O(n)\)이다.
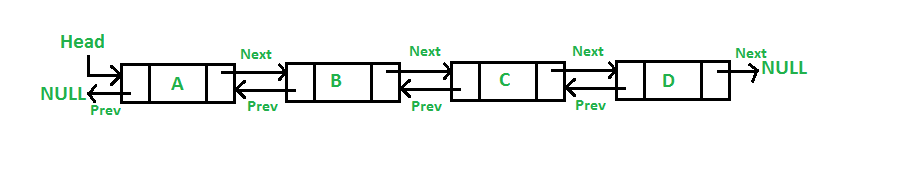
이중 연결 리스트(Doubly linked List)
이중 연결리스트 순회, 삭제, 삽입 구현
class Node:
def __init__(self, data):
self.data = data
self.prev = None
self.next = None
class DoublyLinkedList:
def __init__(self):
self.head = None
def append(self, data):
new_node = Node(data)
if self.head is None:
self.head = new_node
else:
current = self.head
while current.next:
current = current.next
current.next = new_node
new_node.prev = current
def traverse(self):
current = self.head
while current:
print(current.data)
current = current.next
def delete(self, data):
current = self.head
while current:
if current.data == data:
if current.prev:
current.prev.next = current.next
else:
self.head = current.next
if current.next:
current.next.prev = current.prev
break
current = current.next
def insert_after(self, data, new_data):
new_node = Node(new_data)
current = self.head
while current:
if current.data == data:
new_node.prev = current
new_node.next = current.next
if current.next:
current.next.prev = new_node
current.next = new_node
break
current = current.next
# 이중 연결 리스트 인스턴스 생성
doubly_linked_list = DoublyLinkedList()
# 노드 추가
doubly_linked_list.append(1)
doubly_linked_list.append(2)
doubly_linked_list.append(3)
# 순회
print("순회:")
doubly_linked_list.traverse()
# 출력: 1 2 3
# 노드 삭제
doubly_linked_list.delete(2)
# 순회
print("삭제 후 순회:")
doubly_linked_list.traverse()
# 출력: 1 3
# 특정 노드 뒤에 삽입
doubly_linked_list.insert_after(1, 2)
# 순회
print("삽입 후 순회:")
doubly_linked_list.traverse()
# 출력: 1 2 3
이중 연결 리스트 순회/삽입/삭제 코드 구현
