힙(Heap)
힙(Heap) 관련 개념 정리글 입니다.
우선 순위 큐를 위하여 만들어진 자료구조, 힙(heap)에 대해 이해한다.
개념과 종류
개념
- 힙은
완전 이진 트리형태의 자료 구조로, 최댓값 또는 최솟값을 빠르게 찾을 수 있도록 설계되었다. 힙은 일종의 반 정렬 상태(느슨한 정렬 상태) 를 유지한다.
종류
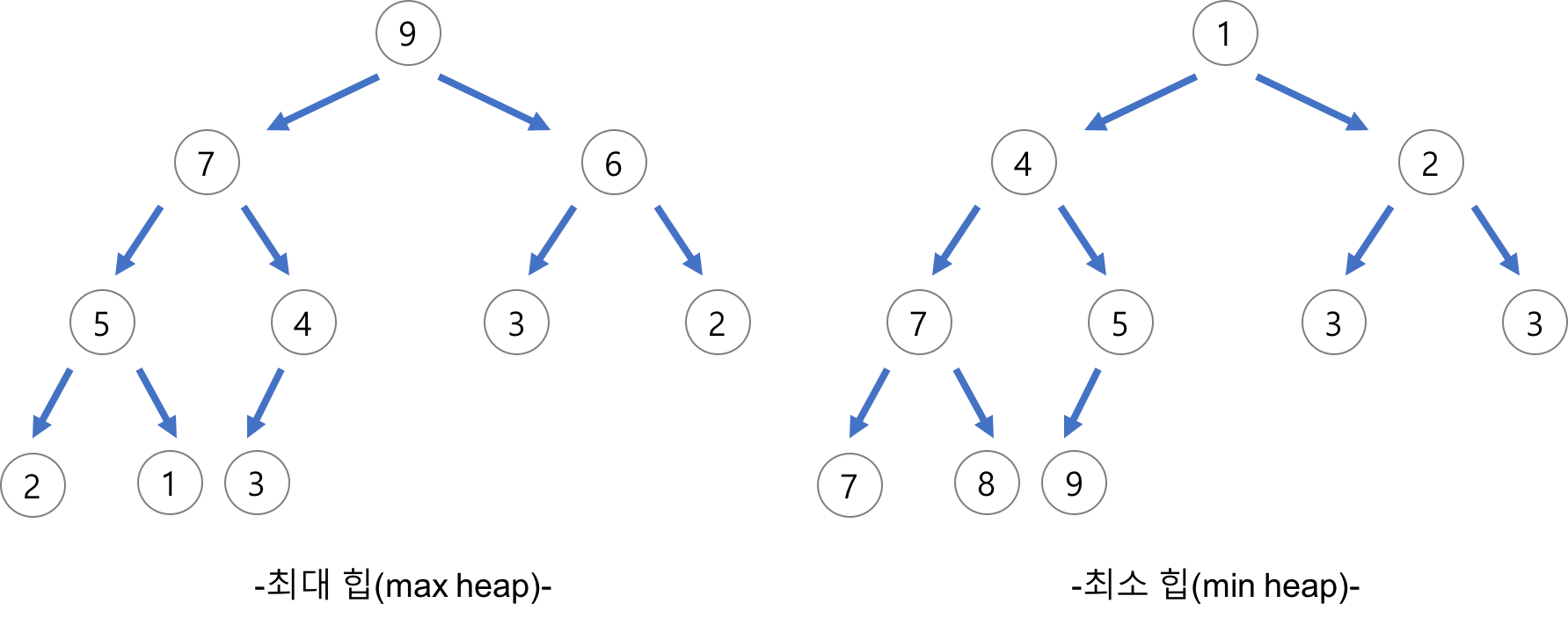
최대 힙(max heap)
- 부모 노드의 키 값이 자식 노드의 키 값보다 크거나 같은 완전 이진 트리
key(부모 노드) >= key(자식 노드)
최소 힙(min heap)
- 부모 노드의 키 값이 자식 노드의 키 값보다 작거나 같은 완전 이진 트리
key(부모 노드) <= key(자식 노드)
동작 원리
삽입
- 힙의 가장 마지막 위치에 요소를 추가한 뒤, 부모 노드와 비교하여 필요한 경우 위치를 조정한다. 이를
"힙의 재구성" 또는 "힙의 상향식 재배치"라고 한다.
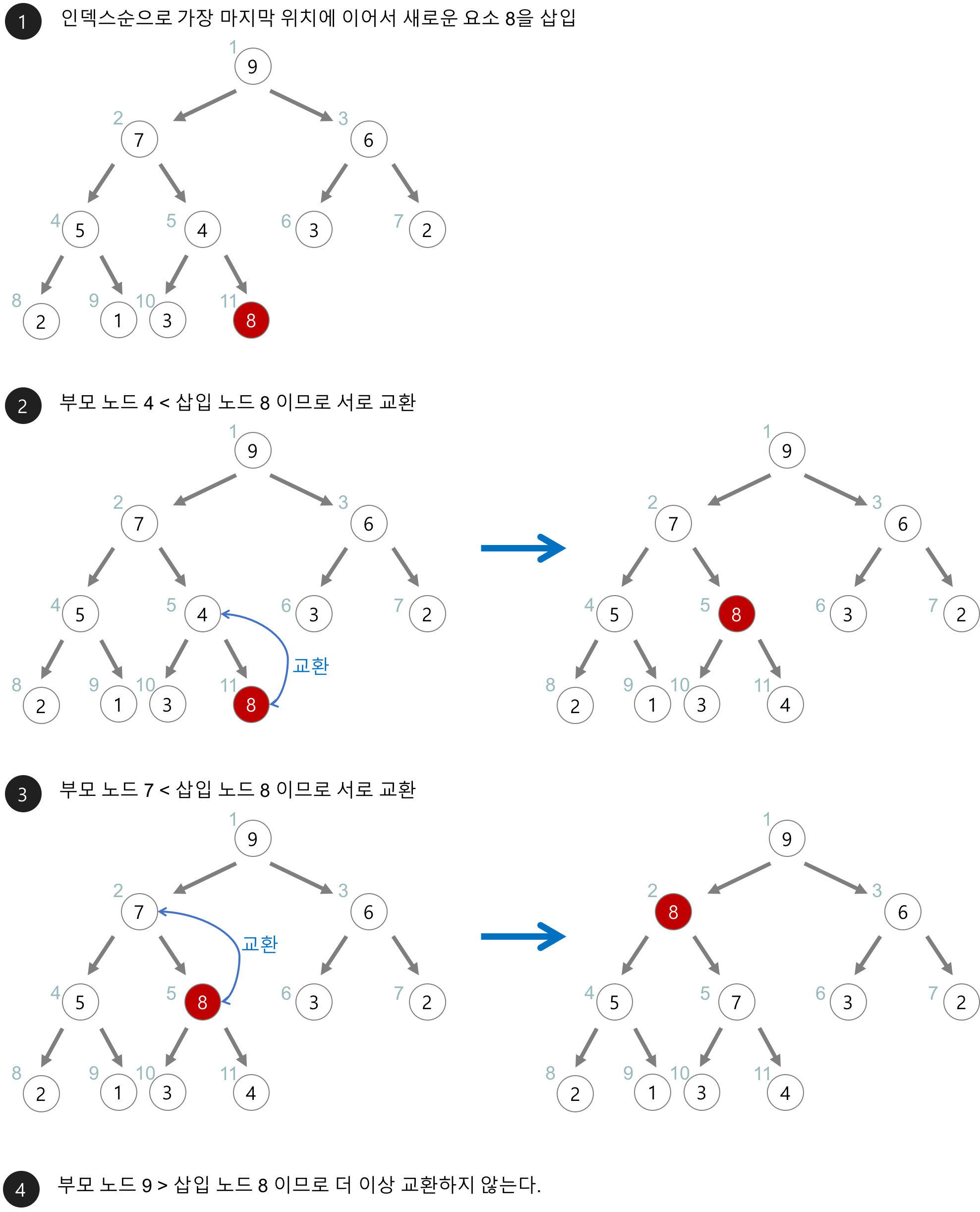
힙의 삽입
삭제
- 루트 노드를 삭제하고, 가장 마지막 위치의 요소를 루트 노드로 옮긴다. 그리고 자식 노드와 비교하여 필요한 경우 위치를 조정한다. 이를
"힙의 재구성" 또는 "힙의 하향식 재배치"라고 한다.
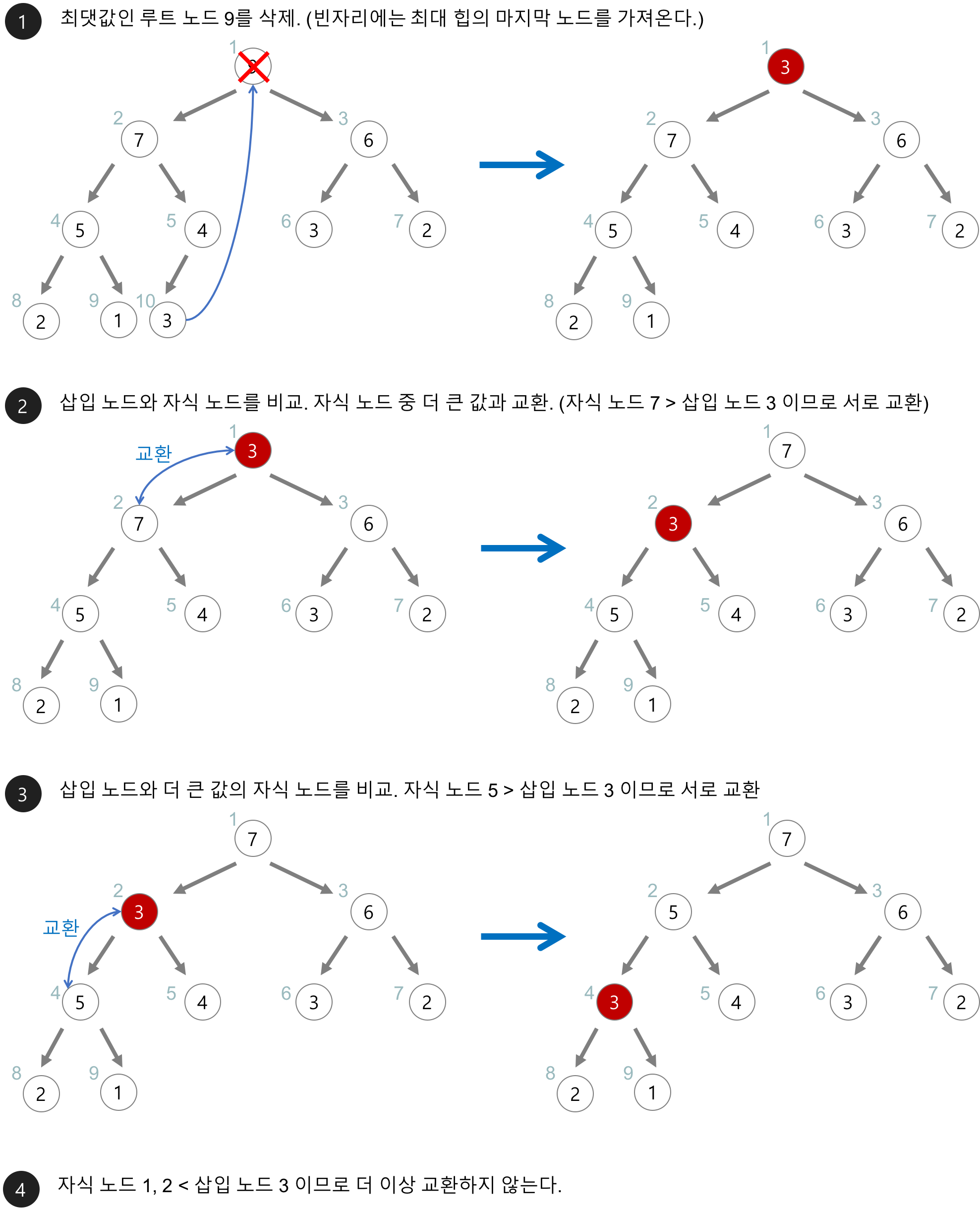
힙의 삭제
구현 방법
1. 배열 기반 힙
class ArrayHeap:
def __init__(self):
self.heap = []
def insert(self, value):
self.heap.append(value)
self._sift_up(len(self.heap) - 1)
def delete(self):
if not self.heap:
return None
self._swap(0, len(self.heap) - 1)
value = self.heap.pop()
self._sift_down(0)
return value
def _sift_up(self, index):
while index > 0:
parent = (index - 1) // 2
if self.heap[index] <= self.heap[parent]:
break
self._swap(index, parent)
index = parent
def _sift_down(self, index):
while index < len(self.heap):
left_child = index * 2 + 1
right_child = index * 2 + 2
largest = index
if left_child < len(self.heap) and self.heap[left_child] > self.heap[largest]:
largest = left_child
if right_child < len(self.heap) and self.heap[right_child] > self.heap[largest]:
largest = right_child
if largest == index:
break
self._swap(index, largest)
index = largest
def _swap(self, i, j):
self.heap[i], self.heap[j] = self.heap[j], self.heap[i]
배열 기반 힙 코드 구현
- 특징
- 힙의 구조를 배열로 표현
- 완전 이진 트리의 성질을 이용하여 부모와 자식 노드의 관계를 인덱스로 계산
- 삽입 연산 시간 복잡도: \(O(log n)\)
- 삭제 연산 시간 복잡도: \(O(log n)\)
- 장점
- 간단한 구현 방법으로 이해하기 쉽다.
- 일반적인 배열의 메모리 캐시 효율을 높일 수 있다.
- 단점
- 배열의 크기를 미리 정해야 하므로 공간 낭비가 발생할 수 있다.
- 삽입 및 삭제 연산 시에 배열 요소의 이동이 필요하므로 시간 복잡도가 높을 수 있다.
- 사용시 좋은 상황
- 배열의 크기가 고정되어야 하는 제약이 없고,
메모리 캐시 효율을 높이고자 할 때유리하다. - 삭제 연산에 대한 성능이 중요하지 않거나
큰 데이터셋을 다룰 때유리하다.
- 배열의 크기가 고정되어야 하는 제약이 없고,
2. 이진 트리 기반 힙
import heapq
class BinaryHeap:
def __init__(self):
self.heap = []
def insert(self, value):
heapq.heappush(self.heap, value)
def delete(self):
if not self.heap:
return None
return heapq.heappop(self.heap)
이진 트리 기반 힙 코드 구현
- 특징
- 파이썬 내장 모듈인 heapq를 활용하여 이진 트리 기반 힙을 구현
- 내장 모듈이므로 구현이 간단하고 효율적이다.
- 최소 힙으로 구현
- 삽입 연산 시간 복잡도: \(O(log n)\)
- 삭제 연산 시간 복잡도: \(O(log n)\)
- 장점
- 내장 모듈인 heapq를 활용하므로 간단하게 구현할 수 있다.
- 자동으로 동적으로 크기가 조절되어 메모리 관리가 용이하다.
- 단점
- 최소 힙으로 구현되어 최대값을 빠르게 찾을 수 없다.
- 구현 방법을 직접 이해하기 어려울 수 있다.
- 사용시 좋은 상황
- 구현이 간단하고 내장 모듈을 활용하기 때문에 빠르게 구현하고자 할 때 유리하다.
- 동적인 크기 조절이 필요하거나 최소 힙을 사용하는 상황에서 유리하다.
- 삭제 연산이 빈번하게 발생하지 않는 경우에 적합하다.
활용 예시
우선순위 큐: 힙을 이용하여 우선순위가 가장 높은 요소에 빠르게 접근할 수 있는 큐를 구현할 수 있다. 예를 들어 작업 스케줄링, 이벤트 처리 등에서 우선순위를 기반으로 작업을 처리해야 할 때 힙을 사용할 수 있다.
힙 정렬: 힙을 이용하여 배열을 정렬하는 힙 정렬 알고리즘은 안정적이고 효율적인 정렬 방법이다. 힙 정렬은 대량의 데이터를 정렬해야 할 때 유용하게 활용될 수 있다.
최댓값 또는 최솟값 검색: 힙은 최댓값 또는 최솟값을 빠르게 찾을 수 있는 자료구조이다. 따라서 최댓값이나 최솟값을 반복적으로 찾아야 하는 상황에서 효율적으로 사용할 수 있다.
