2주차 | 데이터 분석(Data analysis)
KT AIVLE SCHOOL 5기 2주차에 진행한 데이터 분석(Data analysis) 강의 내용 정리 글입니다.
가설 검정
가설과 가설 검정
기존 가설: 정설, 원리, 공식
단서를 통해 가설을 세우고 실험으로 검정
- 모집단(Population)과 표본(Sample)
- 모집단: 우리가 알고 싶은 대상 전체 영역(데이터)
- 표본: 그 대상의 일부 영역(데이터)
- 우리는 일부분으로 전체를 추정하고자 한다
- 모집단에 대한 가설 수립
- 가설은 보통 x와 y의 관계를 표현
- X에 따라 Y가 차이가 있다
- X와 Y는 관계가 있다
- 가설은 보통 x와 y의 관계를 표현
- 표본을 가지고 가설이 진짜 그러한 지 검증(검정)
- 모집단에 대한 가설 수립
- 비즈니스 이해 단계에서 비즈니스 문제로부터 우리의 관심사(Y)를 도출 → Y에 영향을 주는 요인(X)들을 뽑아서 가설 수립
- 귀무가설 \(H_0\): 영가설, 현재의 가설, 보수적인 입장
- 대립가설 \(H_1\): 연구가설, 새로운 가설, 내가 바라는바
- 모집단(Population)과 표본(Sample)
통계적 검정
- 표본으로부터 대립가설을 확인하고, 모집단에서도 맞을 것이라 주장
- 대립가설: 매장 지역(\(x_2\))에 따라 수요량(\(y\))에 차이가 있다
- 귀무가설: 매장 지역(\(x_2\))에 따라 수요량(\(y\))에 차이가 없다
- 분포 + 판단기준 필요
- 차이 값으로부터
p-value계산(차이 값이 클 수록p-value작아짐) - 판단기준(유의수준): 0.05(5%) 혹은 좀 더 보수적인 기준으로 0.01(1%)를 사용
0.05보다는
p-value가 작아야, 차이가 있다고 판단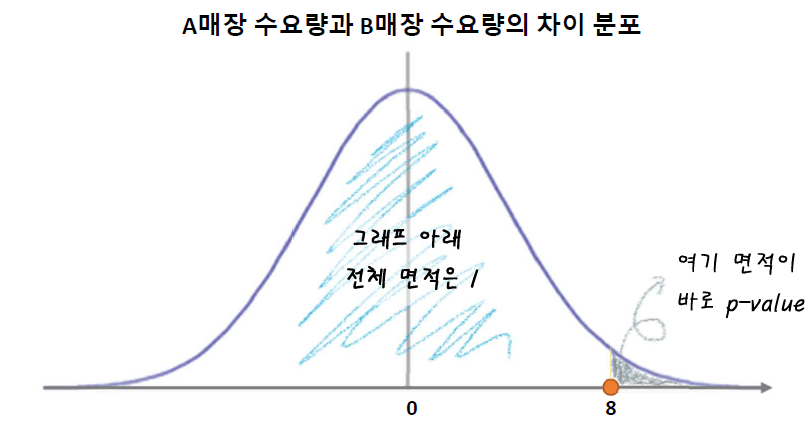
- 차이 값으로부터
- 우리의 관심사가
- A매장과 B매장 중 어디의 수요량이 더 큰가? → 단측검증
매장간의 수요량의 차이가 있나? → 양측검증
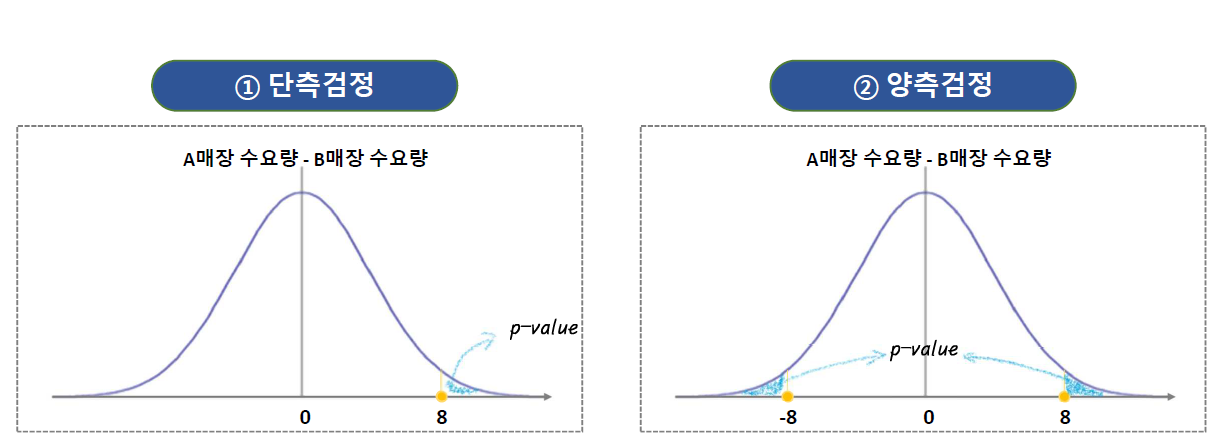
- 검정(차이가 있는지 확인)하기 위한 차이 값(검정 통계량)
t 통계량- \(x^{2}\) (카이 제곱) 통계량
f 통계량
- 이들은 각각 기준 대비 차이로 계산됨
- 계산된 통계량 → 각자의 분포를 가짐
- 분포를 통해서 그 값이 (차이가) 큰지, 작은 지 판단 가능
- 손쉽게 판단할 수 있도록 계산해 준 것이
p-value
- 표본으로부터 대립가설을 확인하고, 모집단에서도 맞을 것이라 주장
이변량 분석 (숫자 → 숫자)
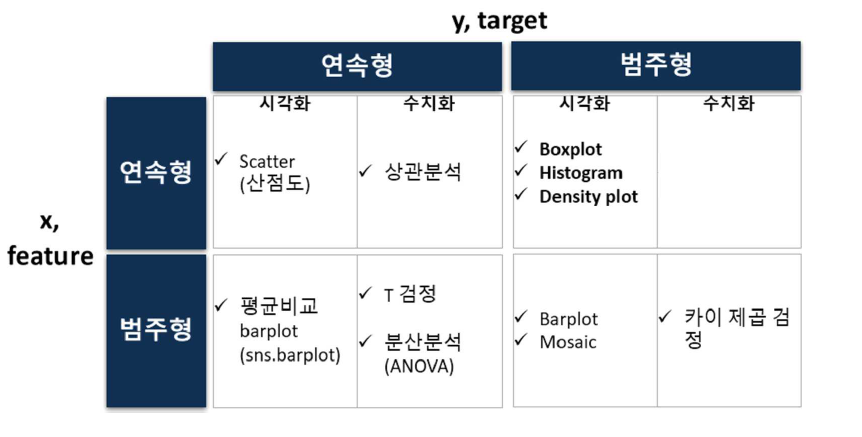
이변량 분석 총정리 표
숫자 vs 숫자 - 정리하는 방법
- 산점도 (그대로 점을 찍어서 그래프를 그림)
- 공분산, 상관계수 (각 점들이 얼마나 직선에 모여 있는지를 계산)
변수 간의 관계를 파악하는 도구들도 각각 한계가 있다 → 보이는게 전부가 아님을 꼭 명심!
시각화: 산점도
- 상관 분석
- 상관 분석은 연속형 변수 X에 대한 연속형 변수 Y의 관계를 분석할 때 사용된다
- Scatter를 통해 시각
- 가설 : 온도(x)가 상승하면 아이스크림 판매량(y)을 증가할까?
- 어떤 관계가 보이나요?
- 얼마나 강한 관계인가요?
숫자 vs 숫자를 비교할 때 중요한 관점:
'직선'(Linearity)
(1) 산점도
- 문법
plt.scatter( x축 값, y축 값 )plt.scatter( ‘x변수’, ‘y변수’, data = dataframe 이름)
- 두 변수의 관계
산점도에서 또렷한 패턴이 보인다면, 강한 관계로 볼 수 있다(특히, 직선의 패턴이 보인다면)
(2) pairplot 한꺼번에 시각화
- 숫자형 변수들에 대한 산점도를 한꺼번에 그려준다
그러나 시간이 많이 걸림
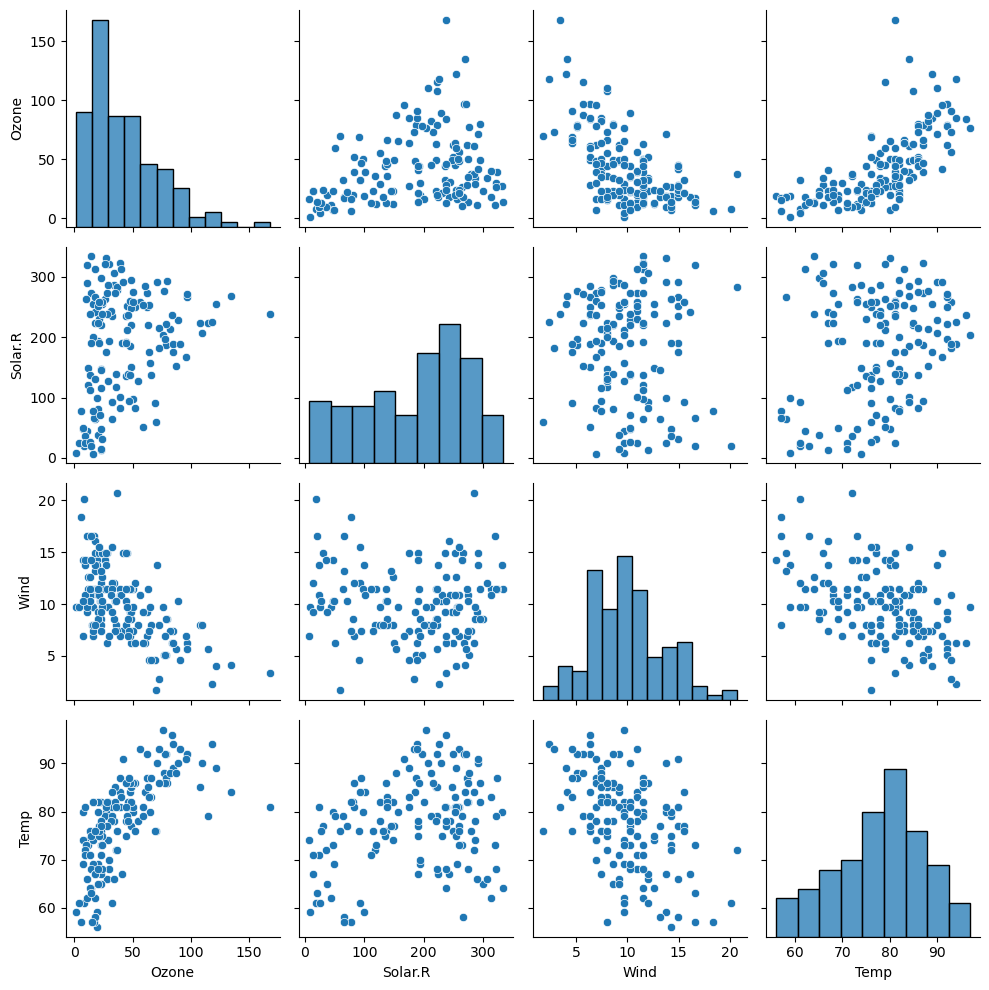
- 아래, 위 중 한쪽을 선택해서 그래프 보기
(3) jointplot, regplot
jointplot은 산점도와 각각의 히스토그램을 함께 보여준다sns.jointplot(x='Temp', y='Ozone', data = air) plt.show()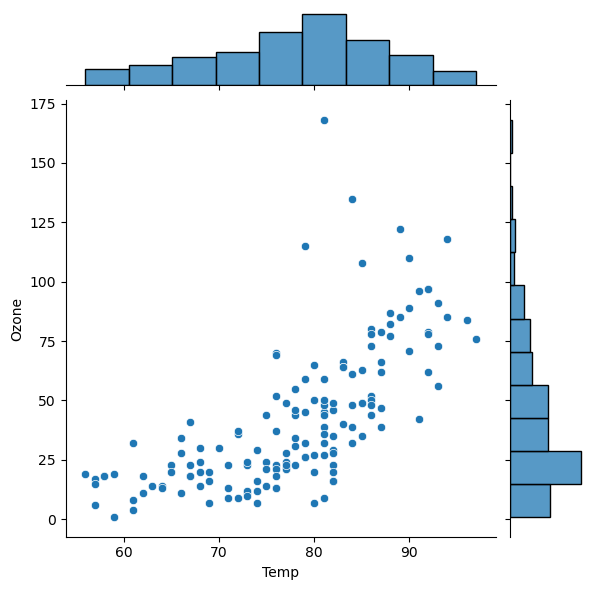
regplotsns.regplot(x='Solar.R', y='Ozone', data = air) plt.show()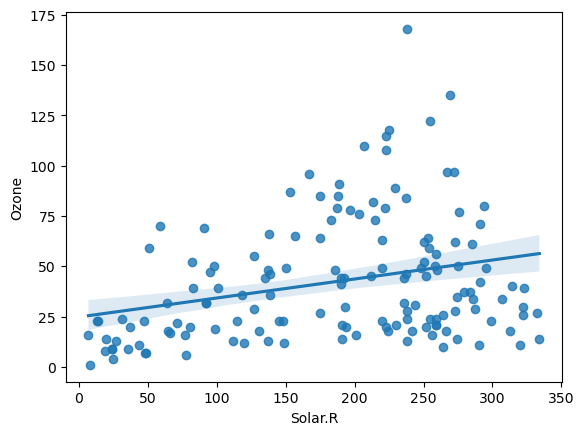
- 장점: 직선을 그려줘서 관계를 잘 알 수 있음
- 단점: 무조건 직선을 그려서 관계가 없어도 있어 보이는 느낌이 든다
수치화 : 상관분석
(1) 상관계수, p-value
- 상관계수 \(r\)
- 공분산을 표준화 한 값
- -1 ~ 1 사이의 값
- -1, 1에 가까울 수록 강한 상관관계를 나타냄
- 경험에 의한 대략의 기준(절대적인 기준이 절대 아님)
- 강한: \(0.5 < \vert r \vert \leq 1\)
- 중간 : \(0.2 < \vert r \vert \leq 0.5\)
- 약한 : \(0.1 < \vert r \vert \leq 0.2\)
- (거의)없음 : \(\vert r \vert \leq 0.1\)
import scipy.stats as spst # 상관계수와 p-value spst.pearsonr(air['Temp'], air['Ozone'])- 결과: 튜플 (상관계수, p-value)
- 첫 번째 값 : 상관계수
- 두 번째 값 : p-value
- 귀무가설 : 상관 관계가 없다 (상관계수가 0이다)
- 대립가설 : 상관 관계가 있다 (상관계수가 0이 아니다)
주의 사항 : 값에 NaN이 있으면 계산되지 않는다 → 반드시
.notnull()로 제외하고 수행해야 한다
(2) 데이터프레임 한꺼번에 상관계수 구하기
air.corr()- 위 결과로 부터,
- 같은 변수끼리 구한 값 1은 의미 없다 (대각선은 의미 없음) → 아래나 위쪽 데이터만 보기
- 상관계수의 절대값이
- 1에 가까울 수록 강한 상관관계
- 0에 가까울 수록 약한 상관관계
- +는 양의 상관관계, -는 음의 상관관계
- 위 결과로 부터,
(3) 상관계수를 heatmap으로 시각화
plt.figure(figsize = (8, 8))
sns.heatmap(air.corr(),
annot = True, # 숫자(상관계수) 표기 여부
fmt = '.3f', # 숫자 포멧 : 소수점 3자리까지 표기
cmap = 'RdYlBu_r', # 컬러맵
vmin = -1, vmax = 1) # 값의 최소, 최대값
plt.show()
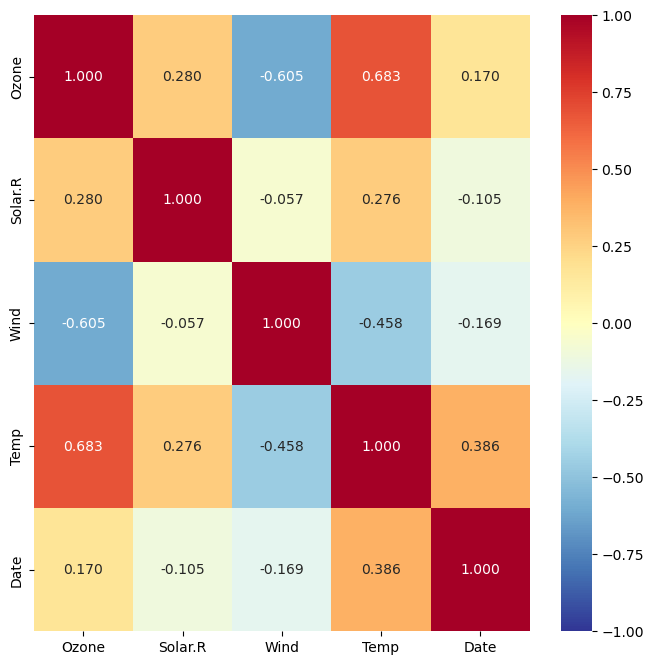
칼라를 변경하려면 아래 링크로 가서 color map 을 확인하고 조정
cmap(color map) : https://matplotlib.org/stable/tutorials/colors/colormaps.html
(4) 상관계수의 한계
- 상관계수는 직선의 관계(선형관계)만 수치화 해준다
- 직선의 기울기, 비선형 관계 → 고려하지 않는다
직선의 기울기와 상관계수는 관련이 없다
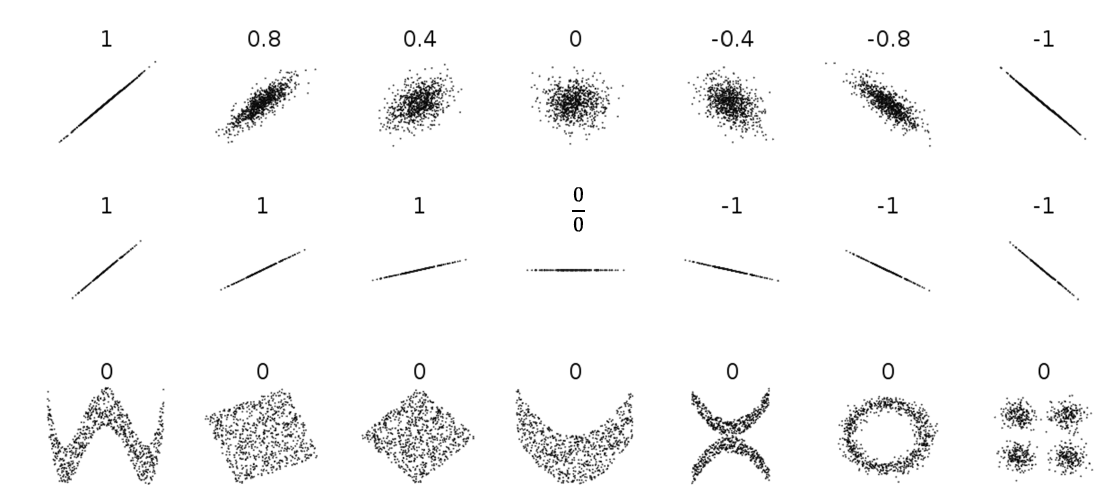
- 산점도와 상관계수를 같이 파악해야 한다
- Focus: 직선 (선형성, Linearity)
- 얼마나 직선으로 잘 설명 가능한가?
- 얼마나 직선에 점들이 모여 있는가?
- 시각화와 수치화를 함께 수행하기
- Focus: 직선 (선형성, Linearity)
이변량 분석 함수(숫자 -> 숫자)
def eda_2_nn(var, target, data):
result = spst.pearsonr(data[var], data[target])
print(f'상관계수 : {result[0]}, p-value : {result[1]}')
sns.scatterplot(x=var, y = target, data = data)
plt.grid()
plt.show()
평균 추정과 신뢰구간
- 평균과 분산, 표준편차
- 분산, 표준편차: 한 집단 설명을 위해 대푯값으로 평균을 계산했을 때 평균으로부터 얼마나 벗어나 있는지를 나타내는 값 (이탈도, deviation)
- 모집단과 표본
- 조사 방법
- 표본 조사
- 추출 방식: 많은 수, 무작위
- 장점: 적절한 비용과 시간
- 단점: 오차가 존재
- 전수 조사
- 전체(모집단)을 조사
- 장점: 정확! 오차: 0
- 단점: 비용, 시간 과다
- 표본 조사
- 표본을 뽑는(표집, sampling) 목적 → 모집단 추정
- 표본을 가지고 어떤 통계량을 계산한다면, 그 목적은 모집단을 추정하기 위함 → 중요
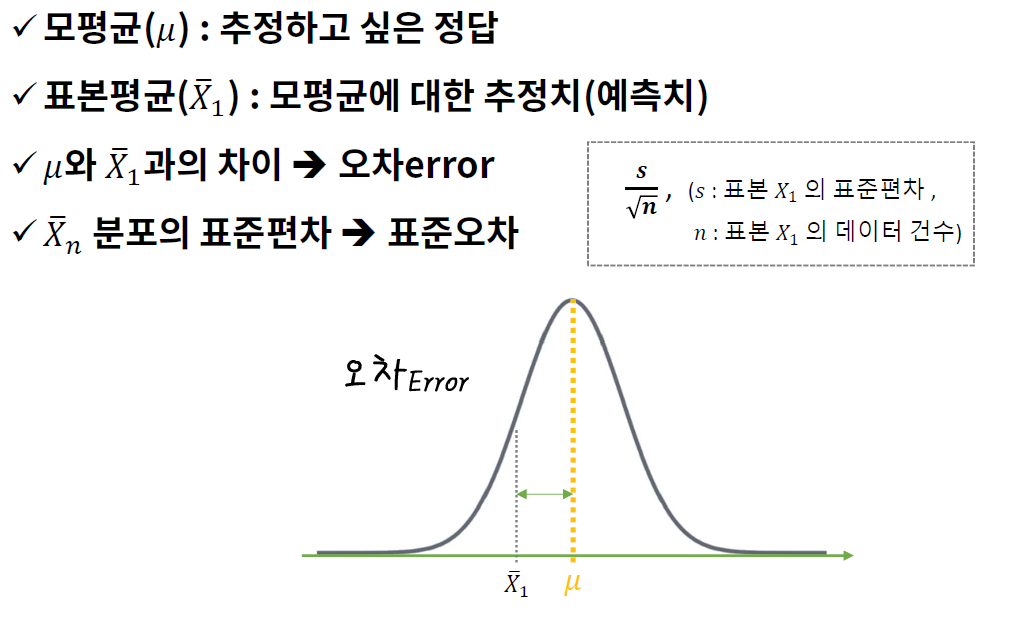
- 표본평균
- 모 평균에 대한 추정치
추정치에는 오차가 존재, 이 오차를 표준오차

- 조사 방법
- 중심 극한 정리 (Central Limit Theorem)
- 표본 평균들의 분포(표집 분포) → 정규분포에 가까워 짐 (모집단의 분포와 상관없이)
- 표본의 데이터 수(표본의 크기) ≥ 30개
- 이 분포(평균들의 분포)의 평균: 모평균에 근사
표본의 크기(\(n\))가 클수록 정규분포 모양이 중심(Central)에 가까워지는(Limit) 좁은 형태가 됨
표준 오차 (Standard Error)
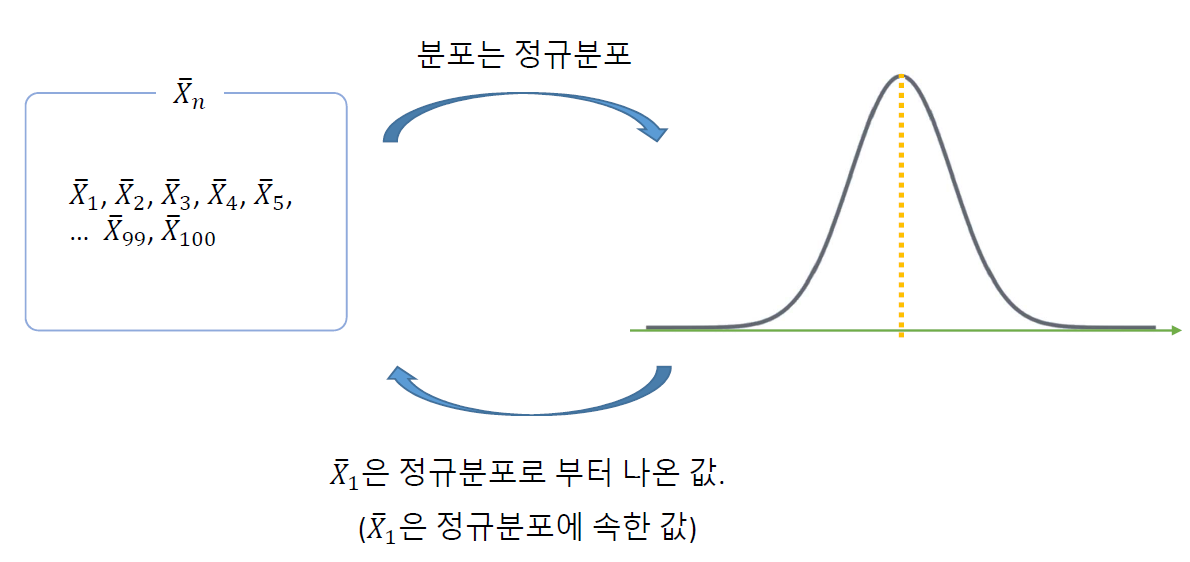
- 표본 평균들의 분포(표집 분포) → 정규분포에 가까워 짐 (모집단의 분포와 상관없이)
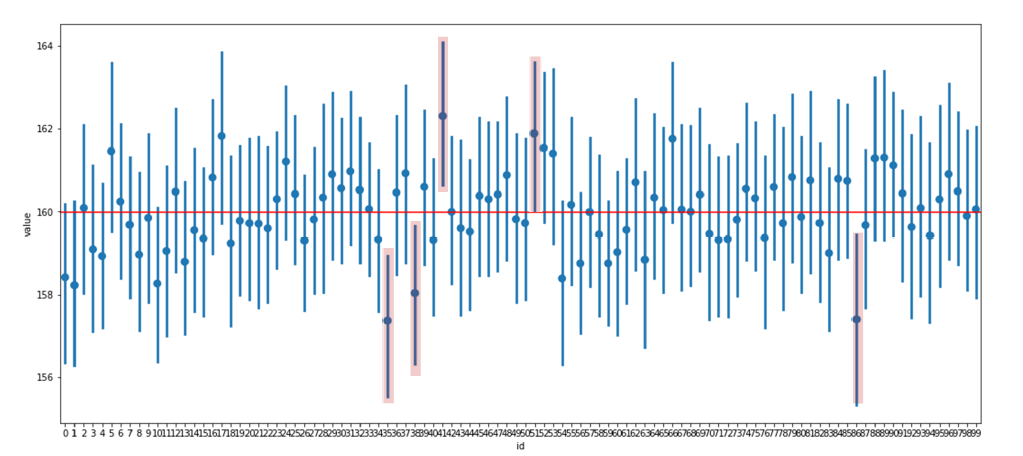
- 95% 신뢰구간 (Confidence Interval)
- 표준오차를 바탕으로 95% 확률 구간을 구할 수 있다
- 95% 신뢰구간의 의미
- 간단한 설명: 신뢰구간 안에 모평균이 포함될 확률이 95%
정확한 설명: 표본을 100번 정도 뽑으면 95번 정도는 95% 신뢰구간 안에 모평균을 포함함
이변량 분석 (범주→ 숫자)
시각화: 두 집단(범주) → 숫자
- 대립가설: 생존여부에 따라 나이의 차이가 있다
(1) 평균 비교 : barplot
- 평균 비교 barplot
- 신뢰구간(오차범위)
- 평균값이 얼마나 믿을 만 한가?
- 좁을 수록 믿을 만 하다
- 데이터가 많을수록, 편차가 적을수록 신뢰구간 좁아짐
두 평균에 차이가 크고, 신뢰구간은 겹치지 않을 때, 대립가설이 맞다고 볼 수 있다
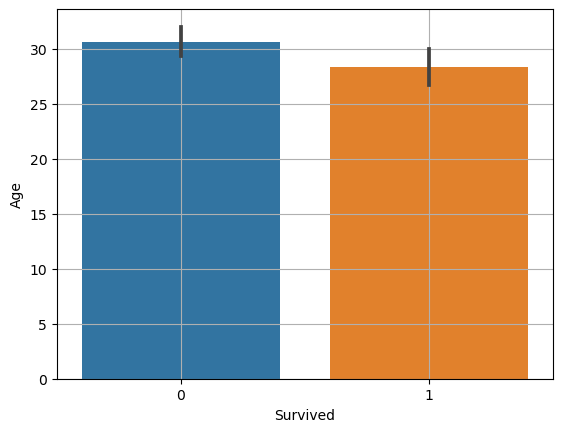
그래프의 검은 선 → 95% 신뢰구간
- 세 집단(범주) → 숫자
- 동일한 함수 사용, 해석 방법도 동일
(2) boxplot
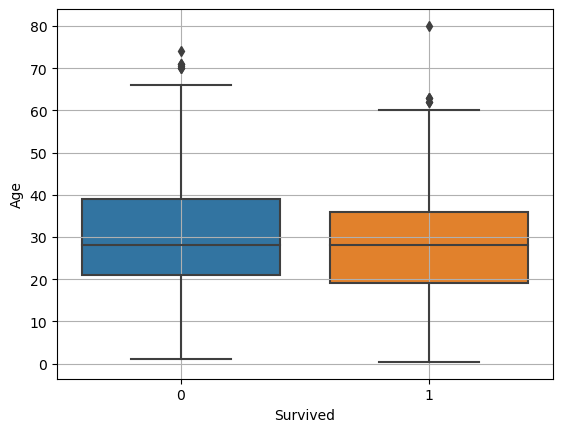
수치화: t-test, anova(분산분석)
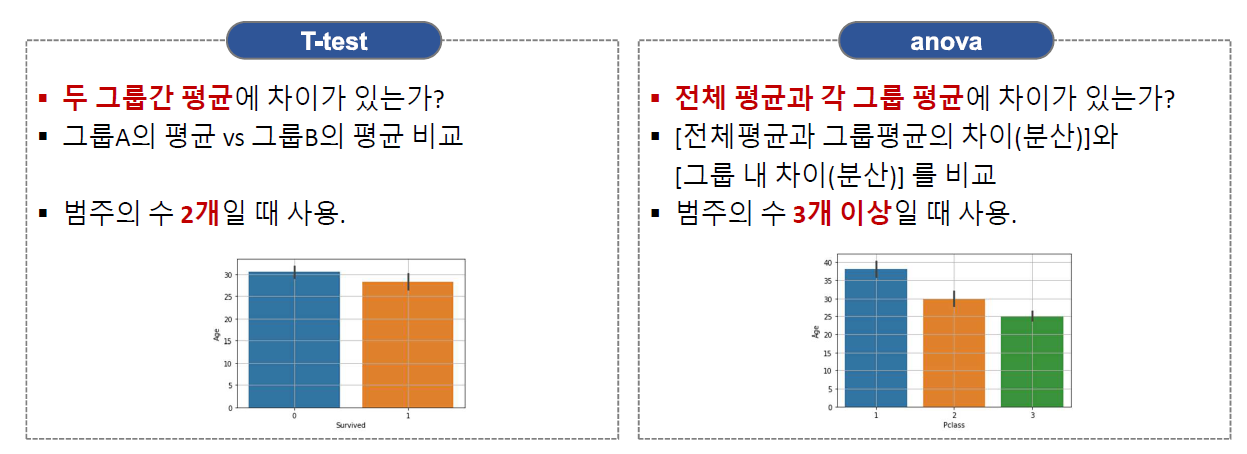
- 범주가 두 개 일 때와 세 개 이상일 때 평균을 비교하는 방법
- t-test와 anova
- 범주형 x와 숫자형 y의 관계를 검정하기 위한 도구
평균을 비교하여 차이 검정(testing)
(1) t-test
- t 통계량
- 두 그룹의 평균 간 차이를 표준오차로 나눈 값
- t 통계량의 분포
- t 통계량이 유의한지 검정
- T-test: t 통계량, p-value
- p-value가 0.05보다 작으면 차이가 있다
- t 통계량이 -2보다 작거나, 2보다 크면, 차이가 있다고 본다
- T-test: t 통계량, p-value
ttest_ind(B, A, equal_var = False)- A와 비교할 때 B의 평균이 큰가?
equal_var: A와 B의 분산이 같은가? 모르면False(default)- 값은 A, B 위치에 따라 부호 반대
- 중요한 것은 차이가 있냐, 없냐 이다
(2) anova
- 분산 분석 ANalysis Of VAriance
- 여러 집단 간에 차이 비교: 기준은 전체 평균
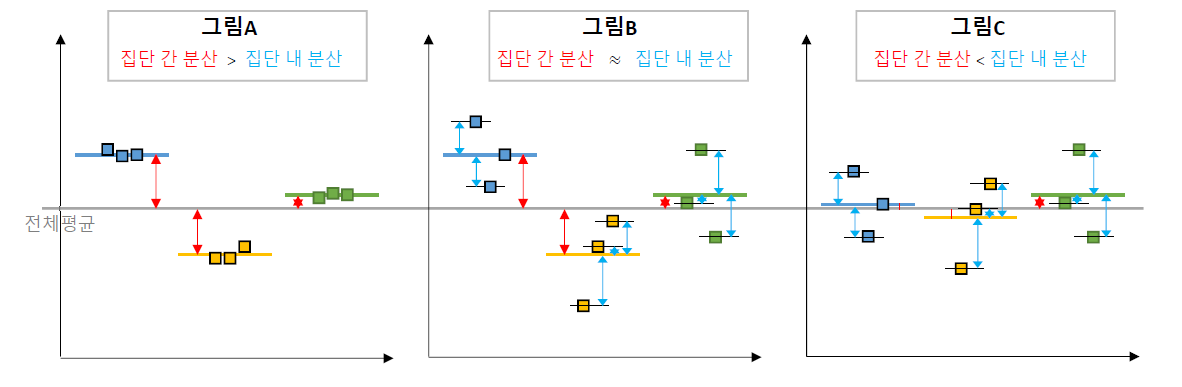
\[𝐹 통계량 = \frac{집단 간 분산}{집단 내 분산} = \frac{전체 평균 − 각 집단 평균}{각 집단의 평균 − 개별 값}\]
값이 대략 2~3 이상이면 차이가 있다고 판단
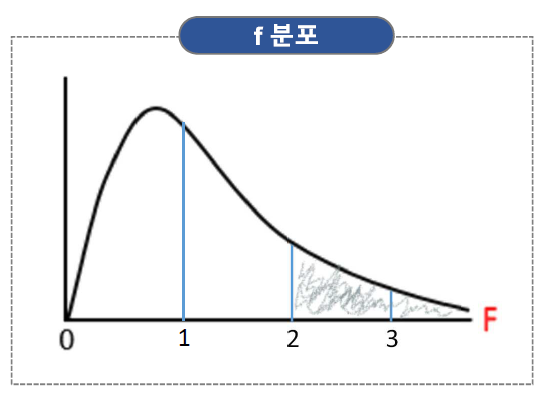
f_oneway(A, B, C)- 전체 평균과 A, B, C 각각의 평균은 차이가 있나?
- 분산분석은 전체 평균대비 각 그룹간 차이가 있는 지만 알려줌
- 그래서, 보통 [사후분석] 진행
이변량 분석 함수(범주 -> 숫자)
def eda_2_cn_ttest(df, var, target):
# Barplot 그리기
sns.barplot(x=var, y=target, data=df)
plt.grid()
plt.show()
# t-test 분석 수행
groups = [df.loc[df[var] == i, target] for i in sorted(df[var].unique())]
t_value, p_value = spst.ttest_ind(*groups)
# 결과 출력
print(f'T-test result for {var}: t-value: {t_value}, p-value: {p_value}')
def eda_2_cn_anova(df, var, target):
# Barplot 그리기
sns.barplot(x=var, y=target, data=df)
plt.grid()
plt.show()
# ANOVA 분석 수행
groups = [df.loc[df[var] == i, target] for i in sorted(df[var].unique())]
f_statistic, p_value = spst.f_oneway(*groups)
# 결과 출력
print(f'ANOVA result for {var}: F-statistic: {f_statistic}, p-value: {p_value}')
이변량 분석 (범주 → 범주)
교차표(crosstab)
- ML에서 사용됨
Pandas의 교차표 함수:crosstab- 두 범주형 변수에 사용 가능
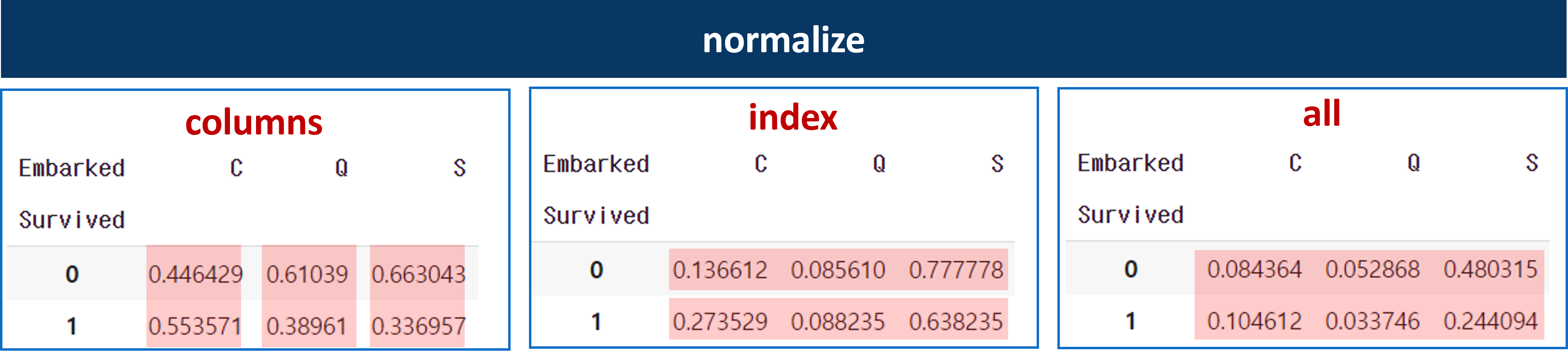
pd.crosstab(titanic['Survived'], titanic['Sex'])normalize옵션: 비율로 변환columns: 열 기준 100%index: 행 기준 100%all: 전체 기준 100%
시각화 (mosaic plot)
mosaic plot: 범주별 양과 비율을 나타냄mosaic(dataframe, [ feature, target])# Pclass별 생존여부를 mosaic plot으로 그려 봅시다. mosaic(titanic, [ 'Pclass','Survived']) plt.axhline(1- titanic['Survived'].mean(), color = 'r') plt.show()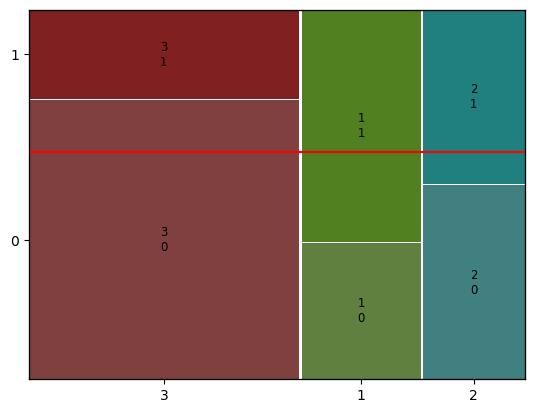
- 빨간선은 전체 평균 (전체 사망률, 전체 생존율)
① X축 길이는 각 객실등급별 승객비율을 나타냅니다.
② 그 중 3등급 객실에 대해서 보면, y축의 길이는, 3등급 객실 승객 중에서 사망, 생존 비율을 의미합니다.
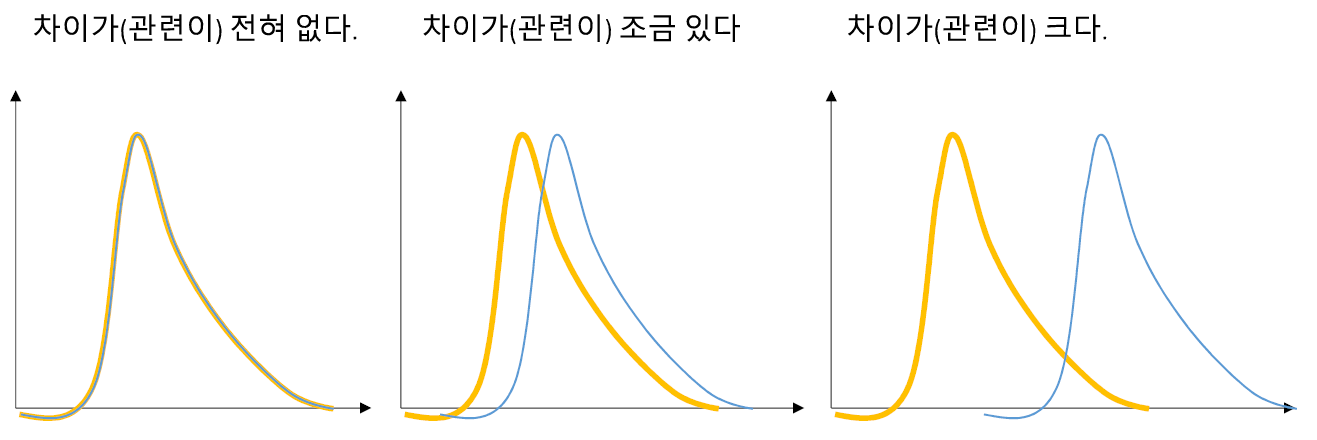
두 범주형 변수가 아무런 상관이 없다면
- 범주 별 비율의 차이가 전혀 없음
- 조금이라도 관련이 있으면, 비율 혹은 bar의 크기에 조금이라도 차이가 남
수치화 (카이제곱검정)
- 카이제곱검정 : 범주형 변수들 사이에 어떤 관계가 있는지, 수치화 하는 방법
- 기대빈도: 아무런 관련이 없을 때 나올 수 있는 빈도수
- 실제 데이터: 관측된 값들
카이제곱 통계량: 기대빈도와 실제 데이터의 차이
\[x^2 = \frac{(관측빈도 - 기대빈도)^2}{기대빈도}\]
- 카이 제곱 통계량은
- 클수록 기대빈도로부터 실제 값에 차이가 크다는 의미
- 계산식으로 볼 때, 범주의 수가 늘어날 수록 값은 커지게 되어 있음
- 보통, 자유도의 2~3배 보다 크면, 차이가 있다고 본다
- 카이 제곱 통계량은
- 범주형 변수의 자유도 : 범주의 수 - 1
- 카이제곱검정에서는
- (x 변수의 자유도) × (y 변수의 자유도)
- ex :
Pclass–>SurvivedPclass: 범주가 3개, Survived : 2개- (3-1) * (2-1) = 2
그러므로, 2의 2 ~ 3배인 4 ~ 6 보다 카이제곱 통계량이 크면, 차이가 있다고 볼 수 있음
# 1) 먼저 교차표 집계 (normalized 옵션 사용하면 안됨) table = pd.crosstab(titanic['Survived'], titanic['Pclass']) print(table) print('-' * 50) # 2) 카이제곱검정 spst.chi2_contingency(table)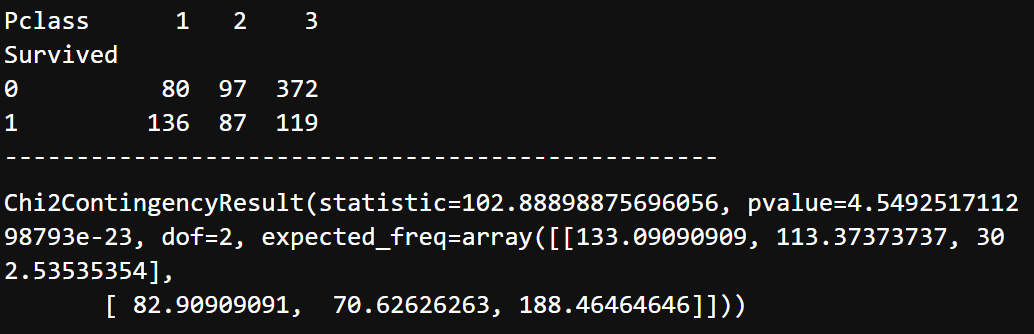
이변량 분석 함수(범주 -> 범주)
def eda_2_cc(feature, target, data):
# 먼저 집계
table = pd.crosstab(data[target], data[feature])
table_norm = pd.crosstab(data[target], data[feature], normalize = 'columns')
print('교차표\n', table)
print('-' * 100)
print('교차표 (norm = columns) \n', table_norm)
print('-' * 100)
mosaic(data, [feature, target])
plt.axhline(1- data[target].mean(), color = 'r')
plt.show()
# 카이제곱검정
result = spst.chi2_contingency(table)
print('-' * 100)
print('카이제곱통계량', result[0])
print('p-value', result[1])
print('자유도', result[2])
print('기대빈도\n',result[3])
이변량 분석 (숫자 → 범주)
시각화
히스토그램을 Survived로 나눠서 그리기
sns.histplot(x='Age', data = titanic, hue = 'Survived') plt.show()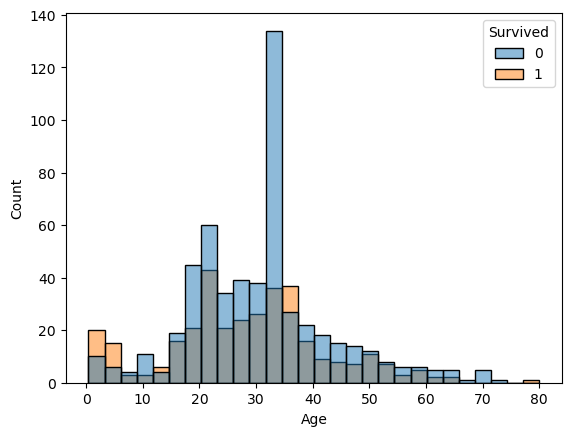
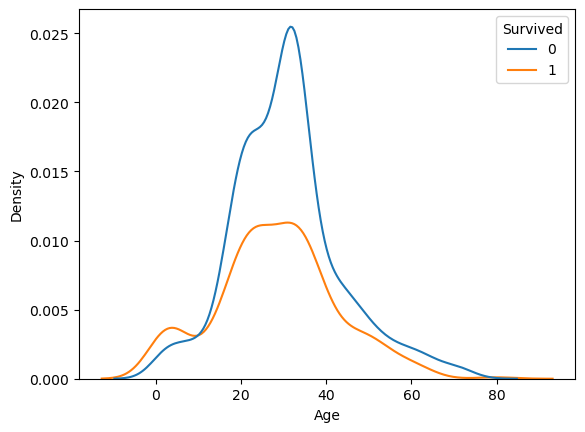
sns.kdeplot()kdeplot( , hue = 'Survived')- 생존여부의 비율이 유지된 채로 그려짐
두 그래프의 아래 면적의 합이 1
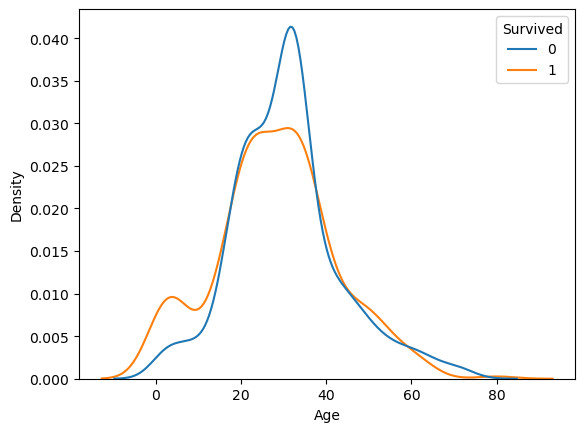
kdeplot( , hue = 'Survived', common_norm = False)common_norm = False: 생존자, 사망자 각각kde plot그리기- 생존여부 각각 아래 면적의 합이 1인 그래프
생존자와 사망자 그래프가 만나는 부분 → 5곳 (전체 평균과 같은 지점)
kdeplot( , hue = 'Survived', multiple = 'fill')multiple = ‘fill’: 모든 구간에 대한 100% 비율로kde plot그리기- 나이에 따라 생존여부 비율을 비교해볼 수 있음. (양의 비교가 아닌 비율!)
빨간선: 전체 평균 생존율
sns.kdeplot(x='Age', data = titanic, hue ='Survived' , multiple = 'fill') plt.axhline(titanic['Survived'].mean(), color = 'r') plt.show()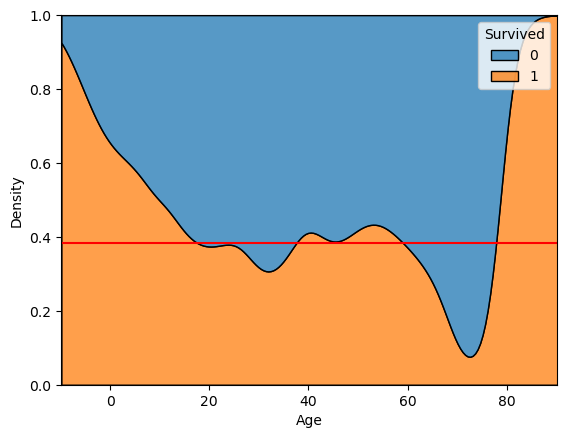
sns.histplot(x='Age', data = titanic, bins = 16 , hue ='Survived', multiple = 'fill') plt.axhline(titanic['Survived'].mean(), color = 'r') plt.show()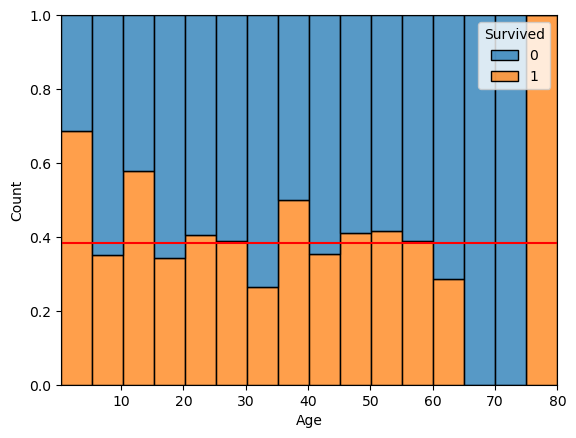
mosaic plot과 비슷한 방식으로 분석
수치형 변수에 따른 범주형 변수의 차이(관련성) 확인
수치화 (미봉책)
- 수치형 X → 범주형 X
- 로지스틱 회귀 (파라미터 p-value 검정)
- 수치형 → 범주형, 범주형 → 수치형
그래프로 판단하는게 더 좋음
이변량 분석 함수(숫자 -> 범주)
def eda_2_nc(feature, target, data):
plt.figure(figsize = (12, 4))
plt.subplot(1, 3, 1)
sns.kdeplot(x= feature, data = data, hue = target,
common_norm = False)
plt.subplot(1, 3, 2)
sns.kdeplot(x= feature, data = data, hue = target
, multiple = 'fill')
plt.axhline(data[target].mean(), color = 'r')
plt.subplot(1, 3, 3)
sns.histplot(x= feature, data = data, hue = target
, multiple = 'fill')
plt.axhline(data[target].mean(), color = 'r')
plt.tight_layout()
plt.show()
